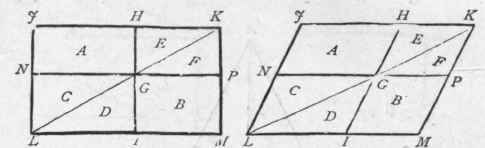
Fig. 256.

341. - Proposition

Parallelograms standing upon the same base and between the same parallels are equal. Let. A BCD and EFCD (Fig. 257) be given parallelograms standing upon the same base, CD, and between the same parallels, A F and CD. Then A B and EF, being equal to CD, are equal to one another; BE being added to both A B and E F, A E equals B F; the line A C being equal to B D, and A E to B F, and the angle C A E being equal (Art. 331) to the angle D B F, the triangle A E C must be equal (Art. 337) to the triangle BED; these two triangles being equal, take the same amount, the triangle B E G, from each, and what remains in one, A B G C, must be equal to what remains in the other, E FD G; these two quadrangles being equal, add the same amount, the triangle C G D, to each, and they must still be equal; therefore, the parallelogram A B CD is equal to the parallelogram EFCD.

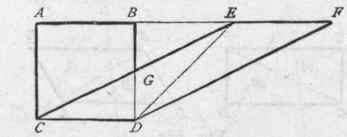
Fig. 257.

Triangle Equal To Quadrangle

342. - Corollary

Hence, if a parallelogram and triangle stand upon the same base and between the same parallels, the parallelogram will be equal to double the triangle. Thus, the parallelogram A D (Fig. 257) is double (Art. 339) the triangle C E D.

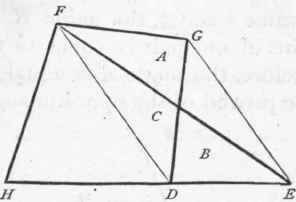
Fig. 258.

343. - Proposition

Let F G HD (Fig. 258) be a given quadrangle with the diagonal F D. From G draw G E parallel to FD; extend HD to E; join Fand E; then the triangle FE H will be equal in area to the quadrangle FGHD. For since the triangles FDG and FDE stand upon the same base, FD, and between the same parallels, FD and G E, they are therefore equal (Arts. 341, 342); and since the triangle C is common to both, the remaining triangles, A and B, are therefore equal; then, B being equal to A, the triangle FE H is equal to the quadrangle F G HD.

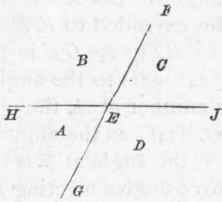
Fig. 259.

344. - Proposition

If two straight lines cut each other, as FG and H J (Fig. 259), the vertical, or opposite angles, A and C, are equal. Thus, FE, standing upon H J, forms the angles B and C, which together amount (Art. 333) to two right angles; in the same manner, the angles A and B form two right angles; since the angles A and B are equal to B and C, take the same amount, the angle B, from each pair, and what remains of one pair is equal to what remains of the other; therefore, the angle A is equal to the angle C. The same can be proved of the opposite angles B and D.

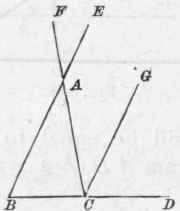
Fig. 260.

345. - Proposition, - The three angles of any triangle are equal to two right angles. Let ABC (Fig. 260) be a given triangle, with its sides extended to F, E and D, and the line CG drawn parallel to BE. As GC is parallel, to EB, the angle at H is equal (Art. 331) to the angle at L; as the lines FC and BE cut one another at A, the opposite angles at M and N are equal (Art. 334); as the angle at N is equal (Art. 331) to the angle at J, the angle at J is equal to the angle at M; therefore, the three angles meeting at C are equal to the three angles of the triangle ABC; and since the three angles at C are equal (Art. 333) to two right angles, the three angles of the triangle ABC must likewise be equal to two right angles. Any triangle can be subjected to the same proof.

346. - Corollary

Hence, if one angle of a triangle be a right angle, the other two angles amount to just one right angle.

347. - Corollary

If one angle of a triangle be a 'right angle and the two remaining angles are equal to one another, these are each equal to half a right angle.

348. - Corollary

If any two angles of a triangle amount to a right angle, the remaining one is a right angle.

349. - Corollary

If any two angles of a triangle are together equal to the remaining angle, that remaining angle is a right angle.

350. - Corollary

If any two angles of a triangle are each equal to two thirds of a right angle, the remaining angle is also equal to two thirds of a right angle.

351. - Corollary

Hence, the angles of an equilateral triangle are each equal to two thirds of a right angle.

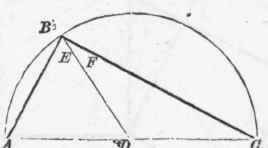
Fig. 261

352. - Proposition

If from the extremities of the diameter of a semicircle two straight lines be drawn to any point in the circumference, the angle formed by them at that point will be a right angle. Let ABC (Fig. 261) be a given semicircle; and A B and B C lines drawn from the extremities of the diameter A C to the given point B; the angle formed at that point by these lines is a right angle. Join the point B and the centre D; the lines DA, D B, and D C, being radii of the same circle, are equal; the angle at A is, therefore, equal (Art. 338) to the angle at F; also, the angle at C is, for the same reason, equal to the angle at F; the angle ABC, being equal to the angles at A and C taken together, must, therefore (Art. 349), be a right angle.

353. - Proposition

The square on the hypothenuse of a right-angled triangle is equal to the squares on the two remaining sides. Let ABC (Fig. 262) be a given right-angled triangle, having a square formed on each of its sides; then the square BE is equal to the squares HC and GB taken together. This can be proved by showing that the parallelogram BL is equal to the square GB; and that the parallelogram CL is equal to the square HC. The angle CBD is a right angle, and the angle A B F is a right angle; add to each of these the angle ABC; then the angle F B C will evidently be equal (Art. 336) to the angle ABD; the triangle FBC and the square G B, being both upon the same base, FB, and between the same parallels, FB and G C, the square G B is equal (Art. 342) to twice the triangle FBC; the triangle ABD and the parallelogram B L, being both upon the same base, B D, and between the same parallels, B D and A L, the parallelogram BL is equal to twice the triangle ABD; the triangles, FBC and ABD, being equal to one another (Art. 337), the square GB is equal to the parallelogram BL, either being equal to twice the triangle FB C or ABD. The method of proving HC equal to C L is exactly similar - thus proving the square B E equal to the squares H C and G B, taken together.