Geometry treats of the properties of magnitudes.

A point has neither length, breadth, nor thickness.

A line has length only.

Superficies has length and breadth only.

A plane is a surface, perfectly straight and even in every direction; as the face of a panel when not warped nor winding.

A solid has length, breadth, and thickness.

A right, or straight, line is the shortest that can be drawn between two points.

Parallel lines are equidistant throughout their length.

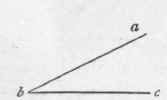
Fig. 327.

Fig. 328,

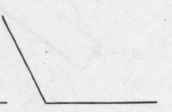
Fig. 329.

An angle is the inclination of two lines towards one another (Fig. 327).

A right angle has one line perpendicular to the other (Fig. 328).

An oblique angle is either greater or less than a right angle (Figs. 327 and 329).

An acute angle is less than a right angle (Fig. 327).

An obtuse angle is greater than a right angle (Fig. 329).

When an angle is denoted by three letters, the middle one, in the order they stand, denotes the angular point, and the other two the sides containing the angle; thus, let a, b, c (Fig. 327) be the angle, then b will be the angular point, and ab and be will be the two sides containing that angle.

A triangle is a superficies having three sides and angles (Figs. 330, 331, 332, and 333).

An equilateral triangle has its three sides equal (Fig. 330). An isosceles triangle has only two sides equal (Fig. 331).

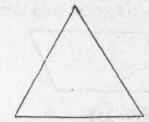
Fig. 330.

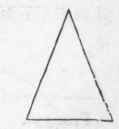
Fig 331.

A scalene triangle has all its sides unequal (Fig. 332). A right-angled triangle has one right angle (Fig. 333). An acute-angled triangle has all its angles acute (Figs. 330 and 331).

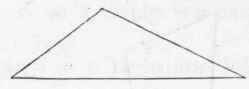
Fig. 332.

Fig. 333.

An obtuse-angled triangle has one obtuse angle (Fig. 332). A quadrangle has four sides and four angles (Figs. 334 to 339).

A parallelogram is a quadrangle having its opposite sides parallel (Figs. 334 to 337).

Fig. 334.

Fig. 335.

A rectangle is a parallelogram, its angles being right angles (Figs. 334 and 335).

A square is a rectangle having equal sides (Fig. 334).

A rhombus is an equilateral parallelogram having oblique angles (Fig. 336).

A rhomboid is a parallelogram having oblique angles (Fig. 337).

A trapezoid is a quadrangle having only two of its sides parallel (Fig. 338).

Fig. 336.

Fig. 337.

A trapezium is a quadrangle which has no two of its sides parallel (Fig. 339).

A polygon is a figure bounded by right lines.

A regular polygon has its sides and angles equal.

An irregular polygon has its sides and angles unequal.

Fig. 338.

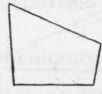
Fig. 330.

A trigon is a polygon of three sides (Figs. 330 to 333); a tetragon has four sides (Figs. 334 to 339); a pentagon has five (Fig. 340); a hexagon six (Fig. 341); a heptagon seven (Fig. 342); an octagon eight (Fig. 343); a nonagon nine; a decagon ten; an undecagon eleven; and a dodecagon twelve sides.

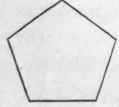
Fig. 340.

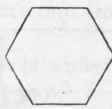
Fig. 341.

Fig. 342.

Fig. 343.

A circle is a figure bounded by a curved line, called the circumference, which is everywhere equidistant from a certain point within, called its centre.

The circumference is also called the periphery, and sometimes the circle.

The radius of a circle is a right line drawn from the centre to any point in the circumference (ab, Fig. 334).

All the radii of a circle are equal. The diameter is a right line passing through the centre, and terminating at two opposite points in the circumference. Hence it is twice the length of the radius (cd, Fig. 344.)

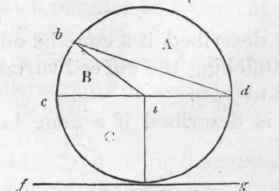
fig. 344.

Fig. 345.

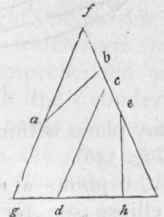
Fig. 346.

A sector is any part of a circle bounded by an arc and two radii, drawn to its extremities (B, Fig. 344).

A quadrant, or quarter of a circle, is a sector having a quarter of the circumference for its arc (C, Fig. 344).

A tangent is a right line which, in passing a curve, touches, without cutting it (fg, Fig. 344).

A cone is a solid figure standing upon a circular base diminishing in straight lines to a point at the top, called its vertex (Fig. 345).

The axis of a cone is a right line passing through it, from the vertex to the centre of the circle at the base.

An ellipsis is described if a cone be cut by a plane, not parallel to its base, passing quite through the curved surface (a b, Fig. 346).

A parabola is described if a cone be cut by a plane, parallel to a plane touching the curved surface (c d, Fig. 346 - cd being parallel to fg).

An hyperbola is described if a cone be cut by a plane, parallel to any plane within the cone that passes through its vertex (eh, Fig. 346).

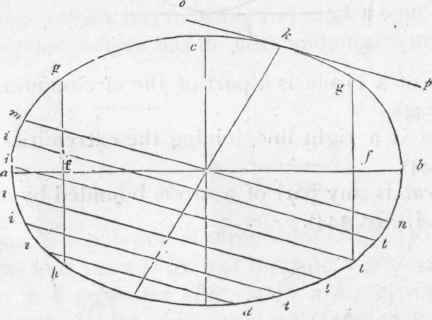
Fig. 347.

Foci are the points at which the pins are placed in describing an ellipse (see Art. 548, and f,f, Fig. 347).

The transverse axis is the longest diameter of the ellipsis (ab, Fig. 347).

The conjugate axis is the shortest diameter of the ellipsis; and is, therefore, at right angles to the transverse axis (cd, Fig. 347).

The parameter is a right line passing through the focus of an ellipsis, at right angles to the transverse axis, and terminated by the curve (gh and gt, Fig. 347).

A diameter of an ellipsis is any right line passing through the centre, and terminated by the curve (kl, or m n, Fig. 347).

A diameter is conjugate to another when it is parallel to a tangent drawn at the extremity of that other - thus, the diameter mn (Fig. 347) being parallel to the tangent op, is therefore conjugate to the diameter kl.

A double ordinate is any right line, crossing a diameter of an ellipsis, and drawn parallel to a tangent at the extremity of that diameter (i t, Fig. 347).

A cylinder is a solid generated by the revolution of a right-angled parallelogram, or rectangle, about one of its sides; and consequently the ends of the cylinder are equal circles (Fig. 348).

Fig. 348.

Fig. 349.

The axis of a cylinder is a right line passing through it from the centres of the two circles which form the ends.

A segment of a cylinder is comprehended under three planes, and the curved surface of the cylinder. Two of these are segments of circles; the other plane is a parallelogram, called by way of distinction, the plane of the segment. The circular segments are called the ends of the cylinder (Fig. 349).

Problems