In computing the transverse stresses in a wooden beam or steel I-beam, it is assumed that the modulus of elasticity is uniform for all stresses within the elastic limit. Experimental tests have shown this to be so nearly true that it is accepted as a mechanical law. This means that if a force of 1,000 pounds is required to stretch a bar .001 of an inch, it will require 2,000 pounds to stretch it .002 of an inch. Similar tests have been made with concrete, to determine the law of its elasticity. Unfortunately, concrete is not so uniform in its behavior as steel. The results of tests are somewhat contradictory. Many engineers have argued that the elasticity is so nearly uniform that it may be considered to be such within the limits of practical use. But all experimenters who have tested concrete by measuring the proportional compression produced by various pressures, agree that the additional shortening produced by an additional pressure, say of 100 pounds per square inch, is greater at higher pressures than at low pressures.

A test of this sort may be made substantially as follows: A square or circular column of concrete at least one foot long is placed in a testing machine. A very delicate micrometer mechanism is fastened to the concrete by pointed screws of hardened steel. These points are originally at a known distance apart - say 8 inches. When the concrete is compressed, the distance between these points will be slightly less. A very delicate mechanism will permit this distance to be measured as closely as the ten-thousandth part of an inch, or to about 1/100,000 of the length. Suppose that the various pressures per

Fig. 92. Transmission of Tension in Steel to Concrete.

100,000 square inch, and the proportionate compressions, are as given in the following tabular form:

We may plot these pressures and compressions as in Fig. 93, using any convenient scale for each. For example, for a pressure of 800 pounds per square inch, we select the vertical line which is at the horizontal distance from the origin O of 800, according to the scale adopted. Scaling off on this vertical line the ordinate .00045, according to the scale adopted for compressions, we have the position of one point of the curve. The other pointsare obtained similarly. Although the points thus obtained from the testing of a single block of concrete would not be considered sufficient to establish the law of the elasticity of concrete in compression, a study of the curves which may be drawn through the series of points obtained for each of a large number of blocks, shows that these curves will average very closely to parabolas that are tangent to the initial modulus of elasticity, which is here represented in the diagram by a straight line running diagonally across the figure.

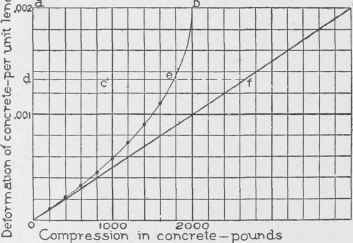
Fig. 93. Curve of Pressures and Compressions.

It is generally considered that the axis of the parabola will be a horizontal line when the curve is plotted according to this method. The position of the vertex of the parabola cannot be considered as definitely settled. Professor Talbot has computed the curve as if the vertex were at the point of the ultimate compression of the concrete, although he conceded that the vertex might be in an imaginary position corresponding to a compression in the concrete higher than that which the concrete could really endure. Mr. A. L. Johnson, another noted authority, bases his computation of formulas on the assumption that the ultimate compressive strength of the concrete is two-thirds of the value which would be required to produce that amount of compression in case the initial modulus of elasticity were the true value for all compressions. In other words, looking at Fig. 93, if o c is a line representing the initial modulus of elasticity, then, if the elasticity were uniform throughout, it would require a force of about 2,340 pounds (or d f) to produce a proportionate compression of .00132 of the length (represented by o d). Actually that compression will be produced when the pressure equals d e, which is 2/3 of d f. It should not be forgotten that the above numerical values are given merely for illustrative purposes. They would, if true, represent a rather weak concrete. The following theory is therefore based on the assumption that the stress-strain curve is represented by the parabolic curve o e (see Fig 93); and that the ultimate stress per square inch in the concrete c' is represented by d e, which is 2/3 of the compressive stress that would be required to produce that proportionate compression if the modulus of elasticity of the concrete were uniformly maintained at the value it has for very low pressures.