An example will be necessary to make this problem clear to the general student.

The nearest corner of a piece of pattern on the carpet is 4 1/2 feet beneath the eye, 2 feet to our right and 3 1/2 feet in direct distance from us. We intend to make a drawing of the pattern which shall be seen properly when held 1 1/2 foot from the eye. It is required to fix the position of the corner of the piece of pattern.

Let A B, Fig. 51., be our sheet of paper, some 3 feet wide. Make S T equal to 1 1/2 foot. Draw the line of sight through s. Produce T S, and make D S equal to 2 feet, therefore T D equal to 3 1/2 feet. Draw D c, equal to 2 feet; C P, equal to 4 feet. Join T C (cutting the sight-line in Q) and T P.

Let fall the vertical Q p', then p' is the point required.

If the lines, as in the figure, fall outside of your sheet of paper, in order to draw them, it is necessary to attach other sheets of paper to its edges. This is inconvenient, but must be done at first that you may see your way clearly; and sometimes afterwards, though there are expedients for doing without such extension in fast sketching.

It is evident, however, that no extension of surface could be of any use to us, if the distance T D, instead of being 3 1/2 feet, were 100 feet, or a mile, as it might easily be in a landscape.

It is necessary, therefore, to obtain some other means of construction; to do which we.must examine the principle of the problem.

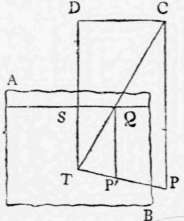
Fig. 51.

In the analysis of Fig. 2., in the introductory remarks, I used the word height only of the tower, Q P, because it was only to its vertical height that the law deduced from the figure could be applied. For suppose it had been a pyramid, as O Q P, Fig. 52., then the image of its side, Q P, being, like every other magnitude, limited on the glass A B by the lines coming from its extremities, would appear only of the length Q' s; and it is not true that Q' S is to Q P as T s is to T P. But if we let fall a vertical Q D from Q, so as to get the vertical height of the pyramid, then it is true that Q' s is to Q D as T S is to T D.

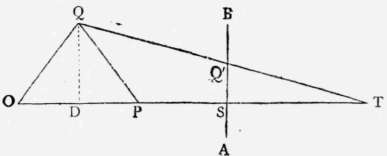
Fig. 52.

Supposing this figure represented, not a pyramid, but a triangle on the ground, and that Q D and Q P are horizontal lines, expressing lateral distance from the line T D, still the rule would be false for Q P and true for Q D. And, similarly, it is true for all lines which are parallel, like Q D, to the plane of the picture A B, and false for all lines which are inclined to it at an angle.

Hence generally. Let P Q (Fig. 2. in Introduction, p. 215) be any magnitude parallel to the plane of the picture; and p' Q' its image on the picture.

Then always the formula is true which you learned in the Introduction: p' Q' is to P Q as S T is to D T.

Now the magnitude P dash Q dash in this formula I call the sight-magnitude of the line P Q. The student must fix this term, and the meaning of it, well in his mind. The sight-magnitude of a line is the magnitude which bears to the real line the same proportion that the distance of the picture bears to the distance of the object. Thus, if a tower be a hundred feet high, and a hundred yards off; and the picture, a piece of glass, is one yard from the spectator,between him and the tower; the distance of picture being then to distance of tower as I to 100, the sight-magnitude of the tower's height will be as I to 100; that is to say, one foot. If the tower is two hundred yards distant, the sight-magnitude of its height will be half a foot, and so on.

But farther. It is constantly necessary, in perspective operations, to measure the other dimensions of objects by the sight-magnitude of their vertical lines. Thus, if the tower, which is a hundred feet high, is square, and twenty-five feet broad on each side; if the sight-magnitude of the height is one foot, the measurement of the side, reduced to the same scale, will be the hundredth part of twenty-five feet, or three inches: and, accordingly, I use in this treatise the term sight-magnitude:'indiscriminately for all lines reduced in the same proportion as the vertical lines of the object If I tell you to find the sight-magnitude of any line, I mean, always, find the magnitude which bears to that line the proportion of S T to D T; or, in simpler terms, reduce the line to the scale which you have fixed by the first determination of the length s T.