If a plane intersects a cone at various angles with the base the geometrical figures thus formed are called conic sections. A plane perpendicular to the base passing through the vertex of a right circular cone forms an isosceles triangle. If the plane is parallel to the base, the intersection of the plane and the conical surfaces will be the circumference of a circle.

Ellipse

If a plane A B, Fig. 85a, cuts a cone oblique to the axis of the cone, but not cutting the base, the curve formed is called an ellipse, as shown in Fig. 85b, this view being taken perpendicular to the plane AB. If the plane cuts a cylinder as shown in Fig. 85c, the ellipse shown in Fig. 85d is the result, this view being also taken perpendicular to the plane AB. An ellipse may be defined as a curve generated by a point moving in a plane in such a man-ner that the sum of the distances from the point to two fixed points shall always be constant.

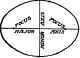
The two fixed points are called foci, Fig. 8G, and shall he on the longest line that can be drawn in the ellipse which is called the major axis; the shortest line is called the minor axis; and is perpendicular to the major axis at its middle point, called the center.

An ellipse may be constructed if the major and minor axes are given or if the foci and one axis are known.

Parabola

If a plane AB, Fig. 87a, cuts a cone parallel to an element of the cone, the curve resulting from this intersection is called a parabola, as shown in Fig. 87b, the view being taken perpendicular to the plane AB. This curve is not a closed curve for the branches approach parallelism. A parabola may be defined as a curve every point of which is equally distant from a line and a point.

The point is called the focus, Fig. 88, and the given line, the directrix. The line perpendicular to the directrix and passing through the focus is the axis. The intersection of the axis and the curve is the vertex.

Hyperbola

If a plane AB, Fig. 89a, cuts a cone parallel to its axis, the resulting curve is called a hyperbola, Fig. 89b, the view being taken perpendicular to the plane AB.

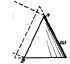
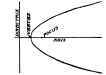
Fig. 88. Diagram Showing Constants of Parabole.

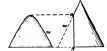
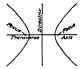
Fig. 95. Diagram Showing Con-atants of Hyperbola.

Like the parabola, the curve is not closed, the branches constantly diverging.

A hyperbola is defined as a plane curve such that the difference between the distances from any point in the curve to two fixed points is equal to a given distance.

The two fixed points are the foci and the line passing through them is the transverse axis, Fig. 90.

Rectangular Hyperbola

The form of hyperbola most used in Mechanical Engineering is called the rectangular hyperbola because it is drawn with reference to rectangular coordinates. This curve is constructed as follows: In Fig. 91, OX and OY are the two coordinate axes drawn at right angles to each other. These lines are also called asymptotes. Assume A to be a known point on the curve. Draw AC parallel to OX and AD' perpendicular to OX. Mark off any convenient points on AC such as E, F, G, and H, and through these points draw EE', FF', GG', and HH', perpendicular to OX. Connect E, F, G, H, and C with 0. Through the points of intersection of the oblique lines and the vertical line A D' draw the horizontal lines LL', MM', NN', PP', and QQ'. The first point on the curve is the assumed point A, the second point is 7?, the intersection of LL' and EE', the third the intersection S, and so on.

In this curve the products of the coordinates of all points are equal. Thus LR x RE' = MS x SF'= NT xTG'.