The Construction Of Regular Polygons. III. - By Means Of The Protractor
Description
This section is from the book "The New Metal Worker Pattern Book", by George Watson Kittredge. Also available from Amazon: The new metal worker pattern book.
The Construction Of Regular Polygons. III. - By Means Of The Protractor
The protractor, which has been already described and illustrated (see Fig. 116, Chapter H), is an instrument for measuring angles. The usual form of this instrument is a semicircle with a graduated edge, the divisions being more or less numerous, according to its size. In instruments of ordinary size the divisions are single degrees, numbered by 5s or by 10s, while in larger sizes the divisions are made to fractions of degrees.
Since the protractor by its construction affords the means of measuring or of setting off any angle whatsoever, it is especially useful in circumscribing or inscribing polygons, or of erecting them upon a given side. As its use is of infrequent occurrence among pattern draftsmen, only a few problems in inscribing will be given, which will be sufficient to enable the reader to apply it in other cases that may arise.
61. To Inscribe an Equilateral Triangle within a Given
Circle. - In Fig. 202, let O be the center of the given circle. Through O draw a diameter, as shown by
COD. Place the protractor so that its center point shall coincide with O, and turn it until the point marking 60 degrees falls upon the line C O D. Then mark points in the circumference of the circle corresponding to 0 (zero) and 120 degrees of the protractor, as shown by B and E respectively. Draw the lines CE, EB and B C, thus completing the required figure. The reasons for these several steps are quite evident. The circle consists of 360 degrees. Then eaeh side of an equilateral triangle must represent one-third of 360 degrees, or 120 degrees. Assume the point C for one of the angles, and draw the line COD. Then, by the nature of the figure to be drawn, D must, fall opposite the center of one side. Therefore, since 60 is the half of 120 (the length of one side in degrees), place 60 opposite the point D, and mark O and 120 for the other angles, then complete the figure by drawing the lines as shown. Since in many cases the protractor is much smaller than the circle in which the figure is to be constructed, it becomes necessary to mark the points at the edge of the instrument, and carry them to the circumference by drawing lines from the center of the circle through the points, producing them until the circle is reached.

Fig. 202. - To Inscribe an Equilateral Triangle within a Given Circle.
62. To Inscribe a Square within a Given Circle. - In Fig. 203, let O be the center of the given circle. Through O draw a diameter, as shown by COD. Place the protractor so that its center point coincides with O, and turn it until the point marking 45 degrees falls upon the line COD. Mark points in the circumference of the circle corresponding to O, 90 and 180 degrees of the protractor, as shown by F, G and E respectively. From G, through the center O, draw G O H, cutting the circumference of the circle in the point
H. Then E, G, F and H are the angles of the required figure, which is to be completed by drawing the sides E G, G F, F H and H E. Since the circle is composed of 360 degrees, one side of an inscribed square must represent one-fourth part of 360 degrees, or 90 degrees. The half of 90 degrees is 45 degrees. Hence, in setting the protractor, the point representing 45 degrees was placed opposite the point in which it is desired the center of one of the sides shall fall, or, in other words, upon the line COD. Then, having marked points 90 degrees removed from each other, or, as explained above, opposite the points 0, 90 and 180 of the protractor, as shown by F, G and E, the fourth point was obtained by the diagonal line. It is evident that 11 must fall opposite G, upon a line drawn through the center. Or the protractor might have been moved around, and a space of 90 degrees measured from either F or E, which, as will be clearly seen, would have given the same point, H.

Fig. 203. - To Inscribe a Square within a Given Circle.
63. To Inscribe an Octagon within a Given Circle-Through the center O of the given circle, Fig. 204, draw a diameter, A O B, upon which the center of one side is required to fall. Place the protractor so that its center point shall coincide with the center O, and turn it so that the point representing 22 1/2 degrees shall fall on the line A O B. Then mark points in the circumference of the circle corresponding to 0, 45, 90, 135 and 180 degrees of the protractor, as shown by E, G, H, I and F. Reverse the protractor, and in like manner mark the points M, Land K; or these points may be obtained by drawing lines from I, H and G respectively through the center O, cutting the circumference in M, L and K. The figure is to be completed by drawing the sides F I, I H, H G, G E,
Geometrial Problems. 59
E M, ML, LK and K F. Since the circle consists of 860 degrees, one side of an octagon must represent 45 degrees, or one-eighth of 860. The half of 45 is 22 1/2. Hence, the point of the protractor representing 224 degrees was placed upon the line A O B, which represents the center of one side of the required figure. Having thus established the position of one side, the other sides of the figure are located by marking points in the circumference of the circle opposite points in the protractor at regular intervals of 45 degrees.
64. To Inscribe a Dodecagon within a Given Circle-In Fig. 205, let O be the center of the given circle.
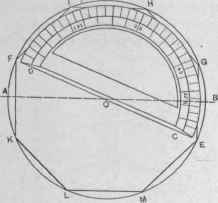
Fig. 204. - To Inscribe an Octagon within a Given Circle.
Through O draw the diameter A O B, at right angles to which one of the sides of the polygon is required to be. Set the protractor so that the center point of it coincides with the center O, and revolve it until the point marking 15 degrees falls upon the line A 0 B. With the protractor in this position, mark points in the circumference of the circle opposite the points in the protractor representing 0, 30, 60, 90, 120, 150 and 180 degrees, as shown by E, F, G, H, I, K and L. Then these points will represent angles of the required polygon. The remaining angles may be obtained by placing the protractor in like position in the opposite half of the semicircle, or they may be determined by drawing lines from the points F,. G, H, I and K through the center O, producing them until they cut the circumference in the points M, N, P, R and S, which are the remaining angles. The figure is now to be completed by drawing the sides, as shown. In ado-decagon, or twelve-sided figure, each side must occupy a space represented by one-twelfth of 360 degrees, or 30 degrees of the protractor. As the side F E was required to be located in equal parts upon opposite sides of A O B, the middle of one division of the protractor representing a side (that is, 15 degrees, or one-half of 30 degrees) was placed upon the line A O B. Having thus established the position of one side, the others are measured off in manner above described.
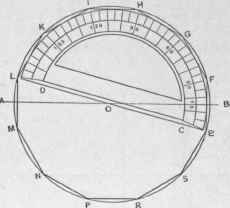
Fig. 205. - To Inscribe a Dodecagon within a Given Circle.
In making use of the protractor to erect a regular polygon upon a given side, the exterior angle, or angle formed by an adjacent side with the given side extended, as E B D in Figs. 168, 170 and 171, is found by dividing 360 degrees by the number of sides in the required polygon; while the interior angle, or angle between any two adjacent sides on the inside of the polygon, as E B A in the same diagrams, is the supplement of that angle, or, in other words, is found by subtracting the exterior angle from 180 degrees. Thus to find the exterior angle by means of which to construct a regular decagon, divide 360 degrees by 10, which gives 36 degrees; while the interior angle is equal to 180 degrees less 36 degrees, which is 144 degrees.
Continue to:


