Draw a perpendicular from a to s (Fig. 4), and make a s equal to 20 min. or to 4/7 of the whole height, a c; draw s 0 at right angles to s a, and equal to 1 1/4 min.; upon 0, with 2 1/2 min. for radius, describe the eye of the volute; about o, the centre of the eye, draw the square, r t 1 2, with sides equal to half the diameter of the eye, viz. 2 1/2 min., and divide it into 144 equal parts, as shown at Fig. 5. The several centres in rotation are at the angles formed by the heavy lines, as figured, 1, 2, 3, 4, 5, 6, etc. The position of these angles is determined by commencing at the point, 1, and making each heavy line one part less in length than the preceding one. No. 1 is the centre for the arc a b (Fig. 4;) 2 is the centre for the arc be; and so on to the last. The inside spiral line is to be described from the centres, x, x, x, etc. (Fig. 5), being the centre of the first small square towards the middle of the eye from the centre for the outside arc. The breadth of the fillet at aj is to be made equal to 2 3/10 min. This is for a spiral of three revolutions; but one of any number of revolutions, as 4 or 6, may be drawn, by dividing of (Fig. 5) into a corresponding number of equal parts. Then divide the part nearest the centre, 0, into two parts, as at h; join 0 and 1, also 0 and 2; draw h 3 parallel to 0 1, and h 4 parallel to 0

Fig. 3. - Grecian Ionic.

Fig. 4. - Ionic Volute.

The Ionic Volute

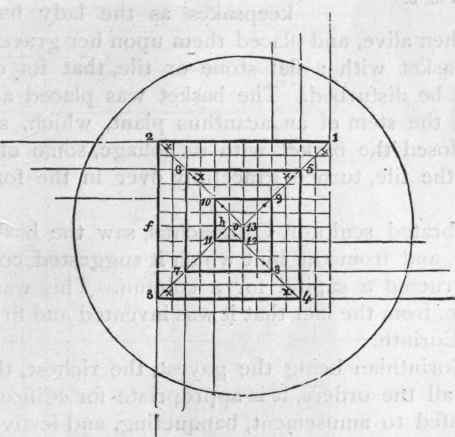
Fig. 5. - Eye of Volute.

2; then the lines 0 1, 0 2, k 3, h 4 will determine the length of the heavy lines, and the place of the centres. (See Art. 288.)

38. - The Corinthian Order: (Fig. 7,) is in general like the Ionic, though the proportions are lighter. The Corinthian displays a more airy elegance, a richer appearance; but its distinguishing feature is its beautiful capital. This is generally supposed to have had its origin in the capitals of the columns of Egyptian temples, which, though not approaching it in elegance, have yet a similarity of form with the Corinthian. The oft-repeated story of its origin which is told by Vitruvius - an architect who flourished in Rome in the days of Augustus Caesar - though pretty generally considered to be fabulous, is nevertheless worthy of being again recited. It is this: A young lady of Corinth was sick, and finally died. Her nurse gathered into a deep basket such trinkets and keepsakes as the lady had been fond of when alive, and placed them upon her grave, covering the basket with a flat stone or tile, that its contents might not be disturbed. The basket was placed accidentally upon the stem of an acanthus plant, which, shooting forth, enclosed the basket with its foliage, some of which, reaching the tile, turned gracefully over in the form of a volute.

A celebrated sculptor, Calimachus, saw the basket thus •decorated, and from the hint which it suggested conceived and constructed a capital for a column. This was called Corinthian, from the fact that it was invented and first made use of at Corinth.

The Corinthian being the gayest, the richest, the most lovely of all the orders, it is appropriate for edifices which are dedicated to amusement, banqueting, and festivity - for all places where delicacy, gayety, and splendor are desirable.