Cones
Description
This section is from the book "Cyclopedia Of Architecture, Carpentry, And Building", by James C. et al. Also available from Amazon: Cyclopedia Of Architecture, Carpentry And Building.
Cones
A cone is a solid bounded by a conical surface and a plane which cuts the conical surface. It may be considered as a pyramid with an infinite number of sides, Fig. SO.
The conical surface is called the lateral area and it tapers to a point called the vertex; the plane is called the base.
The altitude of a cone is the perpendicular distance from the vertex to the base.
An element of the cone is any straight line from the vertex to the circumference of the base.
A circular cone is a cone whose base is a circle
A right circular cone, or cone of revolution, Fig. 81, is a cone whose axis is perpendicular to the base. It may be generated by the revolution of a right triangle about one of the legs as an axis. A frustum of a cone, Fig. 82, is the portion of the cone included between the base and a plane parallel to the base; its altitude is the perpendicular distance between the bases.
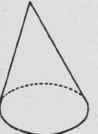
Fig. 80. Cone.

Fig. 81. Right Circular Cone.

Fig. 82. Frustum of Cone.
Continue to:


