True Length Of Lines
Description
This section is from the book "Cyclopedia Of Architecture, Carpentry, And Building", by James C. et al. Also available from Amazon: Cyclopedia Of Architecture, Carpentry And Building.
True Length Of Lines
In Fig. 102 is given the plan and elevation of a square pyramid standing on the horizontal plane. The height of the pyramid is the distance A B. The slanting edges of the pyramid, AC, AD, etc., must be all of the same length, since A is directly above the center of the base. What this length is, however, does not appear in either projection, as these edges are not parallel to either V or H.
Suppose the pyramid be turned around into the dotted position C1h D1h Eth Fth where the horizontal projections of two of the slanting edges, ACth and AE1h, are parallel to the ground line. These two edges, having their horizontal projections parallel to the ground line, are now parallel to V, and therefore their new vertical projections will show their true lengths. The base of the pyramid is still on H, and therefore is projected on V in the ground line. The apex is in the same place as before, hence the vertical projection of the pyramid in its new position is shown by the dotted lines. The vertical projection A C1v is the true length of edge A Ch. Now if it is desired to find simply the true length of A Ch, it is unnecessary to turn the whole pyramid around, as the one line A Ch will be sufficient. The true length of lines may therefore be found in any case by

Fig. 102. Projections of Square Pyramid.

Fig. 103.
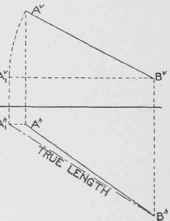
Fig. 104

Fig. 105.
True Length of a Line by Rotating its Projection applying the following principle: Swing one projection of the line par-allel to the groundline, using one end as center. On the other projection the moving end remains at the same distance from the ground line and of course vertically above or below the same end in its parallel position.
This new projection of the line shows its true length, Fig. 103, Fig. 104, and Fig. 105.
Continue to:


