The Distillation And Rectification Of Alcohols By The Rational Use Of Low Temperatures
Description
This section is from "Scientific American Supplement Volumes 275, 286, 288, 299, 303, 312, 315, 324, 344 and 358". Also available from Amazon: Scientific American Reference Book.
The Distillation And Rectification Of Alcohols By The Rational Use Of Low Temperatures
By RAOUL PICTET.
The industrial problem of the rectification of alcohols is based entirely upon the properties of volatile liquids, upon the laws of the maximum tensions of the vapors of these liquids, and upon the influence of temperature upon those different elements which find themselves in presence of each other in an alembic.
If we desire to follow, in their least details, all the phenomena which succeed one another in a rectifying column, and which are connected with one another by a continuous chain of reciprocal influences, the problem becomes exceedingly complex.
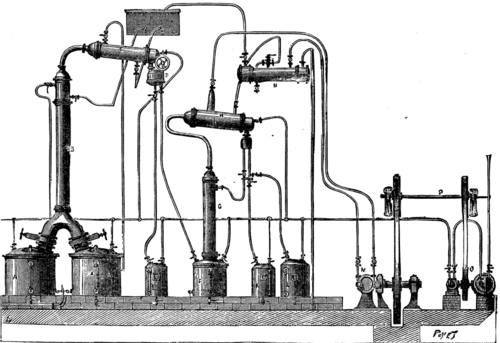
PICTET'S APPARATUS FOR THE RECTIFICATION OF ALCOHOL BY COLD.
In order that the new applications of the mechanical theory of heat may be readily understood, we shall divide this problem into a series of propositions, which we shall examine separately, and which collectively constitutes in its general features the methodical rectification of liquids.
I. Knowing the maximum tensions of pure water and pure alcohol, can we calculate directly the tensions of the vapors of any mixture whatever of alcohol and water?
Yes, we can calculate this tension by a general formula, provided we take into account the affinity of water for alcohol, which increases the value of the total latent heat of evaporation of the liquid. The results of the calculation are fully confirmed by experience. We thus establish the following laws:
a. For any temperature whatever, the maximum tension of the vapors of a mixture of water and alcohol is always comprised between that of pure water and that of pure alcohol.
b. The tension of the vapors of a mixture of water and alcohol approaches the tension of alcohol so much the nearer in proportion as the proof is higher; and, reciprocally, if water is in excess, the tension of the vapors approaches the tension of the vapors of water.
c. The curves of the maximum tensions of vapors formed by all mixtures of alcohol and water are represented by the same general formula, one factor only of which is a function of the richness of the alcoholic solution.
It results, then, from these laws that we may determine with the greatest exactness the richness of a solution containing alcohol and water, if we know the tension of the vapors that it gives off at a certain temperature. Such indications are confirmed by the centigrade alcoholmeter.
We see likewise that, for these solutions of alcohol and water, the laws of Dalton are completely at fault, since the total pressure of the vapors is never equal to the sum of the tensions of the two liquids, water and alcohol.
II. Being given a solution of water and alcohol, mixed in equal volumes, what will be the quality of the vapors emitted from it?
In other terms, do the vapors which escape from a definite mixture of water and alcohol also contain volumes of vapor of water and alcohol in the same proportion as the liquids?
We have discovered the following laws:
d. The quality of the vapors emitted by a mixture of water and alcohol varies according to the alcoholic richness of the solution, but is not in simple proportion thereto.
e. The quality of the vapors emitted by a definite mixture of water and alcohol varies according to the temperature.
f. In a same solution of water and alcohol, it is at low temperatures that the vapors emitted by the mixture contain the largest proportion of alcohol.
g. The more the temperature rises the more the tensions of the two liquids tend to become equalized.
We have been able to verify these different laws experimentally, and to find an interesting confirmation of our general formula of maximum tensions, in the following way:
Let us take a test tube containing a 50 per cent. solution of alcohol and water, plunge it into water of 20°C., and put its interior in hermetic communication with the receiver of a mercurial air-pump.
We vaporize at 20° a certain quantity of the liquid, and the vapors fill the known capacity of the pump. The pressure of the gases in the interior is ascertained by a pressure gauge, and this pressure should be constant if care is taken to act upon a sufficient mass of liquid and with moderate speed. When the receiver of the air-pump is full of vapors, communication between it and the test-tube is shut off, and communication is effected with a second test-tube, like the first, plunged into the same water at 20°. Care must be taken beforehand to create a perfect vacuum in this test-tube.
On causing the mercury to rise into the space that it previously occupied, the vapors are made to condense in the second test-tube at the same temperature as that at which they were formed.
We immediately ascertain that the pressure-gauge shows an elevation of pressure; moreover, the proof of the condensed alcohol has very perceptibly risen.
If, instead of causing these vapors to condense in the second test-tube, we leave the first communication open, the vapors recondense in the first test-tube without any elevation of pressure; and we do not see the least trace of liquid forming in the second test tube.
This difference of pressure in the two foregoing experiments must be attributed, then, to the specific action of the water on the vapors of alcohol. Now we can calculate the difference of the work of the pump, and put at 1 kilogramme of condensed liquid the difference of mechanical work represented in kilogrammeters. What is remarkable is that this difference is absolutely the equivalent of the heat disengaged when the condensed liquid and the old liquid are remixed; there is a complete identity. Thus the affinity of the water for the alcohol modifies the tension of the vapors which form or condense upon the free surface of the mixture. The two phenomena are closely connected by the law of equivalence.
Continue to:


