Wooden And Iron Trusses. Part 3
Description
This section is from the book "Safe Building", by Louis De Coppet Berg. Also available from Amazon: Code Check: An Illustrated Guide to Building a Safe House.
Wooden And Iron Trusses. Part 3
Bearing area.
Bolt at foot.
Calculating strap.
54000/2=27000 pounds on each. The safe shearing stress on wrought-iron being 8000 pounds per square inch (see Table IV) we need an area at each angle = 27000/8000 = 3 3/8 square inches. The strap being 8 inches wide would therefore need to be about 7/16 inch thick.
It was made 1/2 inch, however, as in this case, it was doubtful whether the ironwork would be of a high character. Now each side of the strap will have to withstand a tensional strain of 27000 pounds.
While the safe tension on wrought-iron in Table IV, is 12000 pounds, in this case it was assumed at 9000 pounds only, or the strap needed a sectional area =27000/9000= 3 square inches.
The strap being 1/2 inch thick, would therefore need to be 6 inches wide, to which must be added 1 1/4 inch to allow for bolt holes, making the strap 7 1/4 inches x 1/2 inch. We now settle the number of bolts, which we will make 1 inch diameter.
The safe shearing on a 1 inch bolt will be = 11/18.8000 = 6300 pounds. Each bolt has two shearing areas, one at each end and will therefore resist 12600 pounds.
The total strain being 54000 pounds, we need 54000/12600= 4,3 or say five bolts to resist shearing.
For bearing we have an area 1 inch diameter by 1/2 inch thick against the strap at each end of each bolt, or just one square inch bearing area against iron to each bolt, which will equal a safe resistance to compression of 12000 pounds per bolt, we need therefore
54000/12000 = 4,5 or say five bolts to resist the compression of the strap.
The bolts also bear against the Georgia pine tie-beam and tend to crush it along the grain, the safe resistance of the wood being 750 pounds per square inch. Each bolt bears against 1 inchx 10 inches or 10 square inches of wood, and will safely hear therefore 10.750=7.7500 pounds. We need therefore, to avoid crushing the wood 54000/7500 =7,2 or say eight bolts, which is the number shown in drawing.
Numberof bolts.
We will now similarly analyze an iron truss. This, the same as the above wooden truss, is not intended so much as a guide in designing, as it is as a guide in analyzing the details of each joint. Every truss should be designed with reference to its special duty and position, and joints should be designed in each case to be made up as simply as possible. The designer should not hesitate for fear of criticism as to novelty, to make his truss or its joints of any shape that may be most convenient, bearing always in mind, that the simpler the parts and the nearer to standard sizes, the cheaper will be the execution of the work.
Almost any design can be made by the use of wrought-iron or steel, or of cast-iron.
In the two former, care should be taken to analyze carefully the work required of each rivet. Wrought-iron is gradually taking the place of cast-iron, even for shoes and such parts of trusses, as the expense o riveting them up out of different parts, is apt to be cheaper than the cost of the patterns required for castings.
Iron truss.
F1G.262.
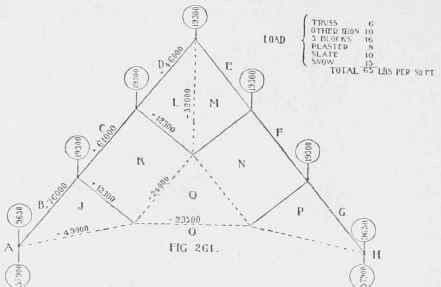
In Figure 261, we have the design of the axial lines of an iron roof truss recently erected in New York City.
The vertical load on this truss was assumed at 65 pounds per square foot and made up as follows :
Vertical load.
Weight of truss | = | 6 | pounds. |
Weight of other iron | = | 10 | pounds. |
Weight of 3 inch blocks | = | 16 | pounds. |
Weight of plaster | = | 8 | pounds. |
Weight of slate | = | 10 | pounds. |
Weight of snow | = | 15 | pounds. |
Total (per square foot) | = | 65 | pounds. |
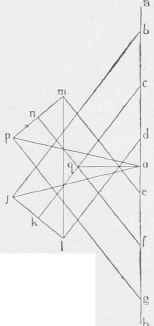
Figure 262 gives the strain diagram for this load; the rafter panels were each 17 feet long, and the trusses placed 17 feet 6 inches from centres, so that the load on each panel was 17.1 7 1/2.65 = 19337 or say 19300 pounds.
The wind-pressure was calculated separately. In Figure 263 it is supposed to blow from the left. The pressure normal to the roof pressure C R till it intersects the horizontal A H at R we obtain the reactions due to wind pressure. As A R measures 40 feet and R H 23 feet, we know that the reaction at H will be surface per square foot for a roof of this inclination (51°) will be, say, 38,4 pounds, (see Table XLIV.)
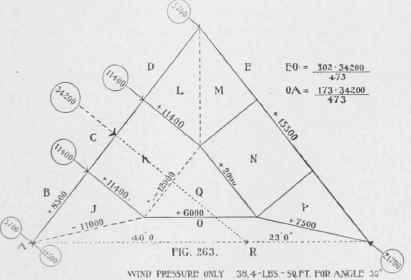
We should have then on each panel: 17.17 1/2.38,4 = 11424 or say 11 100 pounds.
The total wind-pressure therefore was = 34200 pounds. By prolonging the central axis of the wind
Wind pressure.
= 40/63.34200 = 21700 pounds, and at A
= 23/63 .34200 = 12500 pounds. The strain diagram Figure 2G4, can now be easily constructed. We notice that there are no strains in MN nor in NP due to wind; also that the latter reverses the strains in Q N, Q O and P O, they all having to resist compression. In Figure 265 are tabulated the strains due to both vertical load and wind pressure, the last column giving the actual result, that is, their sum or difference, as the case may be. In
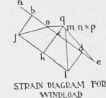
Fig. 264.
Continue to:


