Problem 164. The Envelope Of An Elliptical Cone
Description
This section is from the book "The New Metal Worker Pattern Book", by George Watson Kittredge. Also available from Amazon: The new metal worker pattern book.
Problem 164. The Envelope Of An Elliptical Cone
In Fig. 530 is shown an elevation and plan of a cone whose ba3e is an elliptical figure. So far as the solution of this problem is concerned the plan may be a perfect ellipse or an approximate ellipse drawn by any convenient method. Fig. 531 shows a perspective view of the cone in question, upon which lines have been drawn from points assumed in its base to the apex. From an inspection of this view it will appear that these lines, as in the case of the scalene cone, are of unequal length, and therefore that the pattern of its envelope may be developed by a method analogous to that adopted in the preceding problem.
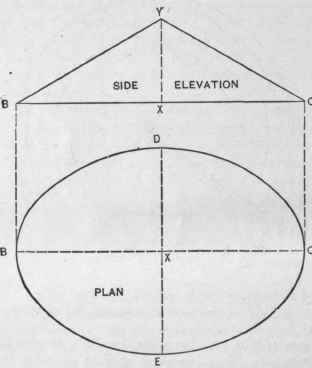
Fig. 530. - Plan and Elevation of Cone with Elliptical Base.
Since the cone consists of four symmetrical quarters, it will be necessary to obtain the envelope of only one quarter, from which the remainder of the pattern can be obtained by reduplication. Therefore draw a half side elevation, as shown by Y X C of Fig. 532, immediately below which draw a quarter plan, X C E, so that the line X C shall be common to both views, as shown. Divide E C into any convenient number of equal parts, as indicated by the small figures. Lines drawn from the points in E C to X will give the base lines of a set of triangles, whose altitudes are equal to the hight of the article X Y, and whose hypothenuses will give the true distances from the apex to the points assumed in the base line. A convenient method for drawing these triangles is as follows: With X as center strike arcs from the points in E C, cutting X C, as shown by the small figures. Lines drawn from the points thus obtained to Y, as shown, will give the hy-pothenuses of the triangles. With Y as center, and the distance from Y to the several points in X C as radii, strike arcs indefinitely. From Y to any point upon the arc 0 draw any line, as Y E, which will form the edge of pattern corresponding to X E of plan. With the dividers set to the space used in stepping off E C of plan, and starting from E of the pattern, space off the stretchout of the plan, stepping from one arc to the next, as shown. From the point 6, or C1, draw a line to Y. Through the points thus obtained trace a line. Then Y C E is the pattern for that part of the article shown on plan by E X C. This quarter can be duplicated by any means most convenient so as to obtain the pattern for one-half or for the whole envelope in one piece, as desired.

Fig. 531. - rerspective View of Cone Shown in Fig. 530 with Lines Drawn upon its Surface Used in Developing Pattern.

Fig. 532. - Pattern of One-Half the Cone Shown in Fig. 530.
Continue to:


