If the size of the disc is required for working up into a circular pan, having a flat bottom and tapered sides, then, with some little modification, the rules, as used in the former case, can be applied. First of all, the mean radius of the pan must be found, and this is done by adding the radius of the bottom to the radius of the top and then dividing by two. The rule for finding the radius of the blank will then read as follows: "Add the square of the bottom radius to twice the product of the mean radius and the slant depth, and extract the square root of the whole." Suppose a pan of this description (Fig. 238) is 2 ft. 6 in. in diameter at the top, 1 ft. 6 in. at the bottom, and 1 ft. 3 in. slant depth.

Let R = radius of disc. " r = mean radius of pan. " r1= radius of bottom. " r2 = radius of top. " s = depth of slant side.

Then the mean radius will be r = r1 + r2 / 2 = 15 + 9 / 2 = 12 in.

The radius of the pattern disc will equal-

The same result can be obtained graphically by the construction shown in Fig. 238. Bisect E F, and draw the line G H through the bisecting point parallel to A B. Draw H J parallel to C A, and thus cut off A J equal to bottom, will give the radius for the blank disc. Any allowance required must, of course, be added on to the pattern, as in the last case.

G H. Using A as centre, and A C as radius, turn A C down, and thus fix the point K. On K J describe a semicircle, and draw the line A L square to A B to meet it. The length of the line drawn from L to F, the centre of the

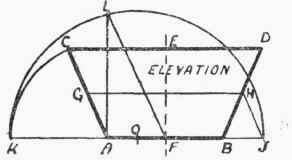
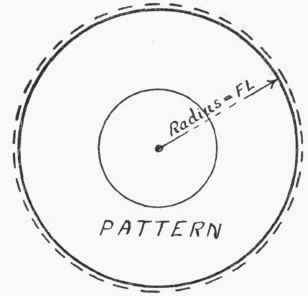
Fig. 238.