Ballistics. Part 7. Drift
Description
This section is from "The Encyclopaedia Britannica". Also available from Amazon: Great Books of the Western World (60 Volumes).
Ballistics. Part 7. Drift
An elongated shot fired from a rifled gun does not move in a vertical plane, but as if the mean plane of the trajectory was inclined to the true vertical at a small angle, 2° or 3°; so that the shot will hit the mark aimed at if the back sight is tilted to the vertical at this angle δ, called the permanent angle of deflection (see Sights).
This effect is called drift and the reason of it is not yet understood very clearly.
It is evidently a gyroscopic effect, being reversed in direction by a change from a right to a left-handed twist of rifling, and being increased by an increase of rotation of the shot.
The axis of an elongated shot would move parallel to itself only if fired in a vacuum; but in air the couple due to a sidelong motion tends to place the axis at right angles to the tangent of the trajectory, and acting on a rotating body causes the axis to precess about the tangent. At the same time the frictional drag damps the nutation and causes the axis of the shot to follow the tangent of the trajectory very closely, the point of the shot being seen to be slightly above and to the right of the tangent, with a right-handed twist. The effect is as if there was a mean sidelong thrust w tan δ on the shot from left to right in order to deflect the plane of the trajectory at angle δ to the vertical. But no formula has yet been invented, derived on theoretical principles from the physical data, which will assign by calculation a definite magnitude to δ.
An effect similar to drift is observable at tennis, golf, base-ball and cricket; but this effect is explainable by the inequality of pressure due to a vortex of air carried along by the rotating ball, and the deviation is in the opposite direction of the drift observed in artillery practice, so artillerists are still awaiting theory and crucial experiment.
After all care has been taken in laying and pointing, in accordance with the rules of theory and practice, absolute certainty of hitting the same spot every time is unattainable, as causes of error exist which cannot be eliminated, such as variations in the air and in the muzzle-velocity, and also in the steadiness of the shot in flight.
To obtain an estimate of the accuracy of a gun, as much actual practice as is available must be utilized for the calculation in accordance with the laws of probability of the 50% zones shown in the range table (see Probability.)
II. Interior Ballistics
The investigation of the relations connecting the pressure, volume and temperature of the powder-gas inside the bore of the gun, of the work realized by the expansion of the powder, of the dynamics of the movement of the shot up the bore, and of the stress set up in the material of the gun, constitutes the branch of interior ballistics.
 Fig. 3.
Fig. 3.
A gun may be considered a simple thermo-dynamic machine or heat-engine which does its work in a single stroke, and does not act in a series of periodic cycles as an ordinary steam or gas-engine.
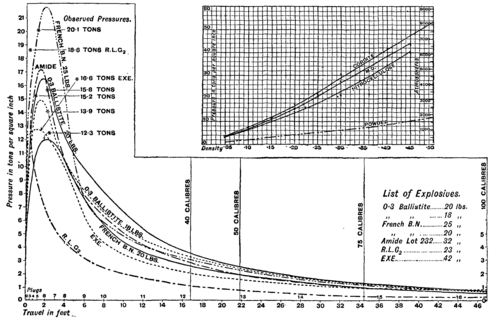 Fig. 4. Pressure Curves, from Chronoscope Experiments in 6 inch gun of 100 calibres, with various Explosives.
Fig. 4. Pressure Curves, from Chronoscope Experiments in 6 inch gun of 100 calibres, with various Explosives.
An indicator diagram can be drawn for a gun (fig. 3) as for a steam-engine, representing graphically by a curve CPD the relation between the volume and pressure of the powder-gas; and in addition the curves AQE of energy e, AvV of velocity v, and AtT of time t can be plotted or derived, the velocity and energy at the muzzle B being denoted by V and E.
After a certain discount for friction and the recoil of the gun, the net work realized by the powder-gas as the shot advances AM is represented by the area ACPM, and this is equated to the kinetic energy e of the shot, in foot-tons,
| (1) e = | w | ( | 1 + | 4k2 | tan2 δ | ) | v2 | , |
| 2240 | d2 | 2g |
in which the factor 4(k2/d2)tan2δ represents the fraction due to the rotation of the shot, of diameter d and axial radius of gyration k, and δ represents the angle of the rifling; this factor may be ignored in the subsequent calculations as small, less than 1%.
The mean effective pressure (M.E.P.) in tons per sq. in. is represented in fig. 3 by the height AH, such that the rectangle AHKB is equal to the area APDB; and the M.E.P. multiplied by ¼πd2, the cross-section of the bore in square inches, gives in tons the mean effective thrust of the powder on the base of the shot; and multiplied again by l, the length in inches of the travel AB of the shot up the bore, gives the work realized in inch-tons; which work is thus equal to the M.E.P. multiplied by ¼πd2l = B - C, the volume in cubic inches of the rifled part AB of the bore, the difference between B the total volume of the bore and C the volume of the powder-chamber.
 Fig. 5. Velocity Curves, from Chronoscope experiments in 6 inch gun of 100 calibres, with Cordite.
Fig. 5. Velocity Curves, from Chronoscope experiments in 6 inch gun of 100 calibres, with Cordite.
Equating the muzzle-energy and the work in foot-tons
| (2) E = | w | V2 | = | B - C | × M.E.P. |
| 2240 | 2g | 12 |
| (3) M.E.P. = | w | V2 | 12 | . |
| 2240 | 2g | B - C |
Working this out for the 6-in. gun of the range table, taking L = 216 in., we find B - C = 6100 cub. in., and the M.E.P. is about 6.4 tons per sq. in.
But the maximum pressure may exceed the mean in the ratio of 2 or 3 to 1, as shown in fig. 4, representing graphically the result of Sir Andrew Noble's experiments with a 6-in. gun, capable of being lengthened to 100 calibres or 50 ft. (Proc. R.S., June 1894).
On the assumption of uniform pressure up the bore, practically realizable in a Zalinski pneumatic dynamite gun, the pressure-curve would be the straight line HK of fig. 3 parallel to AM; the energy-curve AQE would be another straight line through A; the velocity-curve AvV, of which the ordinate v is as the square root of the energy, would be a parabola; and the acceleration of the shot being constant, the time-curve AtT will also be a similar parabola.
If the pressure falls off uniformly, so that the pressure-curve is a straight line PDF sloping downwards and cutting AM in F, then the energy-curve will be a parabola curving downwards, and the velocity-curve can be represented by an ellipse, or circle with centre F and radius FA; while the time-curve will be a sinusoid.
But if the pressure-curve is a straight line F′CP sloping upwards, cutting AM behind A in F′, the energy-curve will be a parabola curving upwards, and the velocity-curve a hyperbola with center at F′.
These theorems may prove useful in preliminary calculations where the pressure-curve is nearly straight; but, in the absence of any observable law, the area of the pressure-curve must be read off by a planimeter, or calculated by Simpson's rule, as an indicator diagram.
To measure the pressure experimentally in the bore of a gun, the crusher-gauge is used as shown in fig. 6, nearly full size; it records the maximum pressure by the compression of a copper cylinder in its interior; it may be placed in the powder-chamber, or fastened in the base of the shot.
Continue to:


