Let e (Fig. 353) be the point above the line c a, from which the perpendicular is required to fall. From c draw any line, as e d, obliquely to the line c a; bisect c d at b; upon b, with the radius be, describe the arc ead; join e and a; then ea will be the perpendicular required.

505. - To Make an Angle (as e df, Fig. 356) Equal to a Given Angle (as b a c). - From the angular point a, with any radius, describe the arc b c; and with the same radius, on the line dc, and from the point d, describe the are fg; take the distance bc, and upon g, describe the small arc at f; join f and d; and the angle edf will be equal to the angle bae.

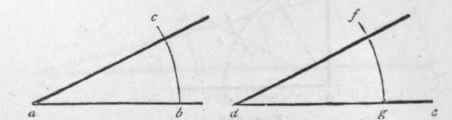
Fig. 356.

If the given line upon which the angle is to be made is situated parallel to the. similar line of the given angle, this may be performed more readily with the set-square. (See Art. 497.)

506. - To Bisect An Angle

Let a be (Fig. 357) be the angle to be bisected. Upon b, with any radius, describe the arc a c; upon a and e, with a radius greater than half a e, describe arcs cutting each other at d; join b and d; and bd will bisect the angle a be, as was required.

Fig. 357.

This problem is frequently made use of in solving other problems; it should therefore be well impressed upon the memory.

507 - To Trisect a Right Angle. - Upon a (Fig. 358), with any radius, describe the arc b c; upon b and c, with the same radius, describe arcs cutting the arc bc at d and e; from d and e draw lines to a, and they will trisect the angle, as was required.

Fig. 358.

The truth of this is made evident by the following operation: divide a circle into quadrants; also, take the radius in the dividers, and space off the circumference. This will divide the circumference into just six parts. A semi-circumference, therefore, is equal to three, and a quadrant to one and a half of those parts. The radius, therefore, is equal to two thirds of a quadrant; and this is equal to a right angle.

508. - Through A Given Point, To Draw A Line Parallel To A Given Line

Let a (Fig. 359) be the given point, and bc the given line. Upon any point, as d, in the line bc, with the radius da, describe the arc ac; upon a, with the same radius, describe the arc de; make de equal to ac; through e and a draw the line ea, which will be the line required. This is upon the same principle as Art. 505.

Fig. 359.

509. - To Divide A Given Line Into Any Number Of Equal Parts

Let a b (Fig. 360) be the given line, and 5 the number of parts. Draw ac at any angle to ab; on ac, from a, set off five equal parts of any length, as at 1, 2, 3, 4 and c; join c and b; through the points 1, 2, 3, and 4, draw 1 e, 2f, 3g and 4h, parallel to cb; which will divide the line ab, as was required.

Fig. 360.

The lines ab and ac are divided in the same proportion. (See Art. 542.)

The Circle

510. - To Find The Centre Of A Circle

Draw any chord, as ab (Fig. 361), and bisect it with the perpendicular cd; bisect cd with the line ef, as at g; then g is the centre, as was required.

Fig. 361.

A second method. Upon any two points in the circumference nearly opposite, as a and b (Fig. 362), describe arcs cutting each other at c and d; take any other two points, as e and f, and describe arcs intersecting, as at g and h; join g and h and c and d; the intersection o is the centre.

Fig. 362.

This is upon the same principle as Art. 514.

A third method. Draw any chord, as ab (Fig. 363), and from the point a draw ac at right angles to ab; join c and b; bisect cb at d - which will be the centre of the circle.

If a circle be not too large for the purpose, its centre may very readily be ascertained by the help of a carpenters'-square, thus: apply the corner of the square to any point in the circumference, as at a; by the edges of the square (which the lines ab and ac represent) draw lines cutting the circle, as at b and c; join b and c; then if bc is bisected, as at d, the point d will be the centre. (See Art. 352.)

Fig. 363.

511. - At A Given Point In A Circle To Draw A Tangent Thereto

Let a (Fig. 364) be the given point, and b the centre of the circle. Join a and b; through the point a, and at right angles to a b, draw cd; then cd is the tangent required.

Fig. 364.

512. - The Same, Without Making Use Of The Centre Of The Circle

Let a (Fig. 365) be the given point. From a set off any distance to b, and the same from b to c; join a and c; upon a, with ab for radius, describe the arc dbc; make db equal to be; through a and d draw a line; this will be the tangent required.

The correctness of this method depends upon the fact that the angle formed by a chord and tangent is equal to any inscribed angle in the opposite segment of the circle (Art. 358); ab being the chord, and bca the angle in the opposite segment of the circle. Now, the angles dab and bca are equal, because the angles dab and bac are, by construction, equal; and the angles bac and bca are equal, because the triangle a bc is an isosceles triangle, having its two sides, ab and bc, by construction equal; therefore the angles dab and bca are equal.

Fig. 365.