Right Lines And Angles
Description
This section is from the book "The American House Carpenter", by R. G. Hatfield. Also available from Amazon: The American House Carpenter.
Right Lines And Angles
500. - To Bisect A Line
Upon the ends of the line ab (Fig. 350) as centres, with any distance for radius greater than half ab, describe arcs cutting each other in c and d;
draw the line cd, and the point e, where it cuts ab, will be the middle of the line ab.
In practice, a line is generally divided with the compasses, or dividers; but this problem is useful where it is desired to draw, at the middle of another line, one at right angles to it. (See Art. 514.)

Fig. 350.
501. - To Erect A Perpendicular
From the point a (Fig. 351) set off any distance, as ad, and the same distance from a to c; upon c, as a centre, with any distance for radius greater than ca, describe an arc at d; upon b, with the same radius, describe another at d; join d and a, and the line da will be the perpendicular required.
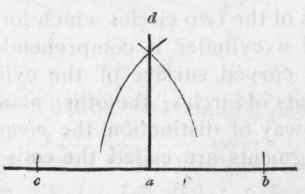
Fig. 351.
This, and the three following problems, are more easily performed by the use of the set-square (see Art. 493). Yet they are useful when the operation is so large that a set-square cannot be used.
502. - To Let Fall A Perpendicular
Let a (Fig. 352) be the point above the line bc from which the perpendicular is required to fall. Upon a, with any radius greater than ad, describe an arc, cutting be at e and f; upon the points e and f, with any radius greater than ed, describe arcs, cutting each other at g; join a and g, and the line ad will be the perpendicular required.
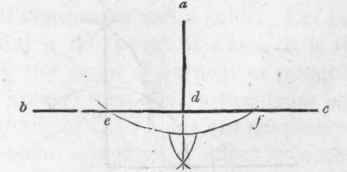
Fig. 352.
503. - To Erect A Perpendicular At The End Of A Line
Let a (Fig. 353), at the end of the line c a, be the point at which the perpendicular is to be erected. Take any point, as b, above the line ca, and with the radius ba describe the arc dae; through d and b draw the line de; join e and a, then e a will be the perpendicular required.

Fig. 353.
The principle here made use of is a very important one, and is applied in many other cases (see Art. 510, 3d, and Art. 513. For proof of its correctness, see Art. 352).
A second method. Let b (Fig. 354), at the end of the line a b, be the point at which it is required to erect a perpendicular. Upon b, with any radius less than b a, describe the arc ced; upon c, with the same radius, describe the small arc ate, and upon e, another at d; upon c and d, with the same or any other radius greater than half e d, describe arcs intersecting at f; join f and b, and the line fb will be the perpendicular required. This method of erecting a perpendicular, and that of the following article, depend for accuracy upon the fact that the side of a hexagon is equal to the radius of the circumscribing circle.

Fig. 354.
A third method. Let b (Fig. 355) be the given point at which it is required to erect a perpendicular. Upon b, with any radius less than b a, describe the quadrant def; upon d, with the same radius, describe an arc at e, and upon e another at c; through d and e draw dc, cutting the arc in c; join c and b, then cb will be the perpendicular required.
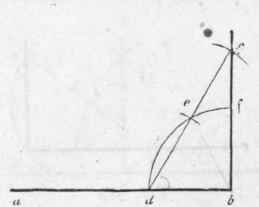
Fig. 355.
This problem can be solved by the six, eight and ten rule, as it is called, which is founded upon the same principle as the problems at Arts. 536, 537, and is applied as follows: let ad (Fig. 353) equal eight, and ae, six; then, if de equals ten, the angle cad is a right angle. Because the square of six and that of eight, added together, equal the square of ten, thus: 6 x 6 = 36, and 8 x 8 = 64; 36 + 64 = 100, and 10 x 10 = 100. Any sizes, taken in the same proportion, as six, eight and ten, will produce the same effect; as 3, 4 and 5, or 12, 16 and 20. (See Art. 536.)
By the process shown at Fig. 353, the end of a board may be squared without a carpenters'-square. All that is necessary is a pair of compasses and a ruler. Let ca be the edge of the board, and a the point at which it is required to be squared. Take the point b as near as possible at an angle of forty-five degrees, or on a mitre-line from a, and at about the middle of the board. This is not necessary to the working of the problem, nor does it affect its accuracy, but the result is more easily obtained. Stretch the compasses from b to a, and then bring the leg at a around to d; draw a line from d, through b, out indefinitely; take the distance db and place it from b to c; join e and a; then ca will be at right angles to ca. In squaring the foundation of a building, or laying out a garden, a rod and chalk-line may be used instead of compasses and ruler.
Continue to:


