Let abed (Fig. 380) be the given circle. Draw the diameter bd; upon b, with the radius of the given circle, describe the arc aec; join a and c, also a and d, and c and d - and the triangle is completed. For the hexagon: from a, also from c, through e, draw the lines af and cg; join a and b, b and c, c and f, etc., and the hexagon is completed. The dodecagon may be formed by bisecting the sides of the hexagon.

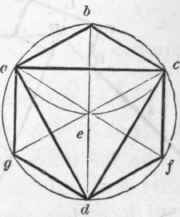
Fig. 380.

Each side of a regular hexagon is exactly equal to the radius of the circle that circumscribes the figure. For the radius is equal to a chord of an arc of 60 degrees; and, as every circle is supposed to be divided into 360 degrees, there is just 6 times 60, or 6 arcs of 60 degrees, in the whole circumference. A line drawn from each angle of the hexagon to the centre (as in the figure) divides it into six equal, equilateral triangles.

528. - Within A Square To Inscribe An Octagon

Let abed (Fig. 381) be the given square. Draw the diagonals a d and b c; upon a, b, c, and d, with a e for radius, describe arcs cutting the sides of the square at 1,2, 3, 4, 5, 6, 7, and 8; join 1 and 2, 3 and 4, 5 and 6, etc., and the figure is completed.

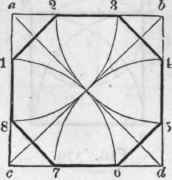
Fig 381.

In order to eight-square a hand-rail, or any piece that is to be afterwards rounded, draw the diagonals a d and b c upon the end of it, after it has been squared-up. Set a gauge to the distance ae and run it upon the whole length of the stuff, from each corner both ways. This will show how much is to be chamfered off, in order to make the piece octagonal (Art. 354).

Fig. 382.