Overhanging Oblong Shoot Or Hopper
Description
This section is from the book "Practical Sheet And Plate Metal Work", by Evan A. Atkins. Also available from Amazon: Practical Sheet And Plate Metal Work.
Overhanging Oblong Shoot Or Hopper
This example (Fig. 55) has been chosen to show the laying out of the plate patterns by turning back from the plan; also, and principally, to illustrate the obtaining of the corner angle-iron rakes by a second method more adaptable for workshop use, in many jobs, than that shown in Figs. 51 and 52.
The patterns are shown laid out in thick dotted lines, the lengths for their widths being obtained as before. Thus, A B = a b', and b c = b' c', from which DC = D c. So with the other pair of plates.
To obtain a corner angle, set the compasses at any distance, and mark off equal lengths Ed ,Ed along E B and E C. Draw perpendiculars to the last two lines through the points d, d, so getting the points f and e. Now take f as centre and f d as radius, and swing on to the line E b, thus obtaining point g. (If the point e be also taken as centre, and e d as radius, this will likewise give point g; hence it will be seen that the latter point can be obtained by the intersection of the arcs, without the use of line E b.) The angle f g e will represent the rake of the corner angle-iron, so that a template can be made to this, to which the angle-iron can be opened.
The application of the above method to finding the acute angle between the front and side plates is, perhaps, not so easily followed as for the back and side plates; it will therefore be an advantage to go over the construction for one of the front angles. Again referring to Fig. 55: Mark F h along both F H and F G to any convenient length. Draw h k square to F G, and h l square to F H, giving the points k and l. Take k as centre, and k h as radius, and swing down the arc on to the line F t, thus obtaining the point n. Join n to l and k to n, producing the latter line, say, to m. Then angle l n m will give the rake of the angle-iron for this corner. The construction lines for obtaining the angles on the other pair of corners are also shown; but, after what has already been said there should be no need for further explanation.
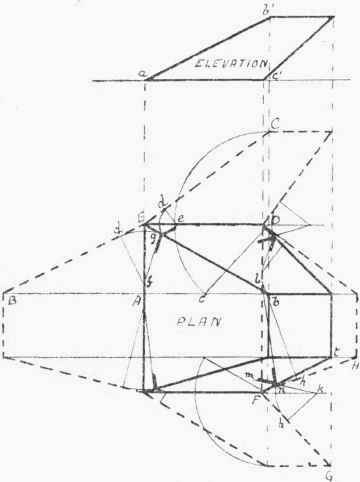
Fig. 55.
Irregular = shaped Bonnet.
In Fig. 56 the plan and elevation of an unequal tapering bonnet or uptake is shown. The bottom and top are both square, but as they are not parallel the bonnet cannot be considered as part of a pyramid.
The plate shapes for back and front can be laid out as in Figs. 54 and 55. The side plates "B" and "D," however, on account of the twist, will require to be set out by the method of triangulation.
Let us take plate "B" first. Draw along B A equal to b a. Mark c a along the base line from c', and then join a' to c". Set the compasses to the length of a' c", and, taking A as centre (on the pattern "B"), draw an arc (shown passing through C). Now open the compasses to the length of
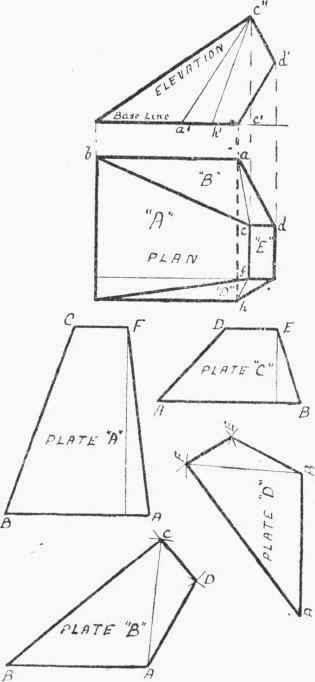
Fig. 56.
B C on the pattern "A," and, using this as a radius from the centre B, cut the first-drawn arc, so obtaining the point C. Fix the compasses to the length c" d', and, taking C as centre, draw an arc (shown passing through D); then, setting the compasses to the length A D on the pattern "C," use this as a radius from centre A to fix the point D. Thus the pattern is complete.
For the pattern "D," the line A B = a b. A F will be the same length as the corresponding line on pattern "A" and B E the same as the similarly lettered line on pattern "C." To obtain the length of B F, mark f h along the base line from c', and join h' to c"; then h' c" will be the true length of B F. Having the lengths of all the lines, the pattern can be laid out in the same way as for plate "B."
To bring the plates "B" and "D" correctly into position, it will be seen that there must be a slight bend about the lines A C and B F. In cases like the above, however, where the twist is slight, there will be no need to kink the plates before bolting together; the screwing up should be sufficient to pull the plates into position.
For articles of any description whose surfaces are twisted similar to above, the method of triangulation can always be applied in the laying out of the plate shapes.

Fig. 57.
Continue to:


